发现自己 LCT 学得太垃圾,于是来做几个题.
LCT 的讲解推荐 FlashHu 大佬的博客 ,讲得很细致. 只是打标记和我的习惯不太一样
QTREE6
开两棵 LCT ,分别维护白点,黑点的信息,询问的答案就是 $u$ 所在的连通块大小.
这可以通过维护虚儿子的大小和得出.
修改时,需要将 $u$ 在某棵 LCT 中断掉,在另一棵 LCT 中加入,如果每次暴力修改,会被菊花图卡掉.
我们常常把边 $u\to v$ 的贡献放到点 $v$ 上来统计,这里可以将 $u$ 的信息放到边 $fa(u)\to u$ 上统计.
即,在白点的 LCT 中,若边 $fa(u)\to u$ 存在,说明 $u$ 为白色.这样修改时就只需要删一条边,加一条边了.
询问时,由于根节点的边 $fa(root)\to root$ 不存在,说明根的颜色与 $u$ 不同,它的所有儿子不能连起来.
于是还需要把根给去掉,在 findroot(u) 找到根后,把它 Splay 上来,它的右儿子就是 $u$ 所在的子树.
需要给原图加一个虚点,表示原图树根的父亲.
时间复杂度 $O(n\log n)$ .
QTREE7
和 QTREE6 大同小异,只是把连通块大小换成了连通块内点权最大值.
用 multiset 维护虚儿子贡献上来的最大值,其它部分同 QTREE6 .
时间复杂度 $O(n\log^2 n)$ .
bzoj 1969 航线规划
LCT 维护边双信息.
如果把每个边双缩成一个点,容易证明会形成一个森林,而答案就是两点所在边双在树上的距离.
于是我们可以用 LCT 来动态维护这个森林,但因为删边后,原来缩起来的点可能会裂开,不好维护,所以只能支持加边.
可以把操作离线下来,倒着做,就只有加边操作了.
在 LCT 中连接 x,y 两个点时,若它们相同,说明原来要连的那两个点已经在一个边双中了,直接跳过.
否则,若还未连通,那么可以直接把它们 link 起来.
若已连通,说明 x 到 y 路径上所有点会形成一个边双.
用 split 将这些点放入一个 splay 中, dfs 这个 splay ,把点都缩到 splay 的根上,再把这个根和它的儿子断开.
可以用并查集来维护每个点被缩到哪个点上去了.
注意 Access 在向上跳时,要跳到父亲被缩到的点,否则新加的实边就会连向已经被缩掉的点,维护的信息就不对了.
时间复杂度 $O(n\log n)$ .
Loj 2245 魔法森林
LCT 动态维护最小生成树.
可以考虑从小到大枚举 $a$ ,那么就会不断加入能用的边.
$a$ 已经被枚举了,只需要最小化 $b$ ,可以维护一棵最小瓶颈生成树, $1$ 到 $n$ 树上路径中 $b$ 的最大值就是需要的 $b$ .
而最小生成树一定也是最小瓶颈生成树,所以用 LCT 动态维护最小生成树即可.
加入一条边 $(u,v)$ 时,若它们已经连通,则需要找出 $u\to v$ 路径上最长的边,若比当前边长,则用当前边替换它.
边权不方便处理,可以对每条边 $(u,v)$ 新建一个点插在 $(u,v)$ 中,就变成维护点权了.
时间复杂度 $O(m\log n)$ .
Loj 2230 大融合
LCT 维护子树信息.
答案显然为以 $y$ 为根时,子树 $x$ 的大小乘上 (子树 $y$ 的大小减去子树 $x$ 的大小) .
需要不断加边,并查集显然没法维护上面那个东西,考虑用 LCT 来维护.
每个节点维护 siz 表示 LCT 中所有儿子信息和时,再维护一个 si 表示所有虚儿子的 siz 之和.
虚儿子的信息只可能在 Access,link 操作时发生变化,此时更新一下 si 就可以了.
Loj 558 我们的 CPU 遭到攻击
LCT 维护子树信息.
把边拆成点,变成维护路径点权之和.
由于 LCT 支持换根,所以只需要分别维护出一棵 Splay 中所有点到深度最小,最大的点的距离和,翻转的时候交换.
为了能合并 Splay 左右儿子的信息,还需要维护出子树内黑点的数目,虚边的子树内黑点到对应子树根的距离和.
当虚边被更改时将对应信息更新就可以了,时间复杂度 $O(n\log n)$ .
Uoj 207 共价大爷游长沙
LCT 维护子树信息.
若一条边 $(x,y)$ 被所有路径经过,则当以 $x$ 为整棵树的根时,每条路径恰有 $1$ 个端点在子树 $y$ 中.
两个元素是否在同一侧的问题,可以用一个经典小 trick ,给每条路径的两个端点异或上一个随机权值.
那么当子树 $y$ 中所有点的异或值恰好等于所有路径权值的异或值时,就说明每条路径恰有 $1$ 个端点在子树 $y$ 中.
用 LCT 维护加边,删边,换根,修改点权,询问子树点权异或和这些操作,时间复杂度 $O(n\log n)$ .
Loj 2001 树点涂色
利用 LCT 中辅助树 Splay 的性质.
每种颜色的点一定会构成一条深度严格递增的链,这和 LCT 中每棵 Splay 维护的东西是一样的.
而每次染色操作,由于是新的颜色,所以等价于进行了一次 Access(x) .
于是可以用 LCT 来维护这些操作,需要维护出每个点到根的颜色种类 $tot$ ,即到根经过的轻边数目 + 1.
每次切换轻重边时,某个子树内的 $tot$ 会 $+1$ 或者 $-1$ ,可以用线段树维护.
注意需要找到 Splay 中深度最小的点,修改它的子树.
对于操作 $2$ , $(x,y)$ 路径上颜色数目就是 $tot(x)+tot(y)-2\cdot tot(lca(x,y))+1$ .
注意这里不能直接 split(x,y) ,因为我们维护的是有根树,这样会改变树的形态.
对于操作 $3$ ,答案就是 $x$ 子树中 $tot$ 的最大值,可以在更新 $tot$ 时用线段树一起维护.
Loj 2092 大森林
LCT + 扫喵线.
有时间和树的编号两个维度,一起维护不太可做,考虑去掉一个维度.
注意到长出的子节点编号只与操作次数有关,可以让每次都给所有树生长出一个新点.
这样不在 $[l,r]$ 内的树会有冗余节点,但只要不把生长节点换成它们,它们就不会对询问产生影响.
可以把每个编号的点实际存在的区间 $[l_x,r_x]$ 记录下来,对 $[l,r]$ 修改生长节点为 $x$ 时,需要将它与 $[l_x,r_x]$ 取并.
而询问操作的答案不会随着之后的操作变化,可以离线下来,最后再一起回答.
可以先把节点长好,再处理生长节点的修改,以及回答询问.
每次修改生长节点时,新建一个虚点,生长点的时候,新建一个实点接在最近的虚点上,把所有虚点按时间顺序串起来.
类似扫描线,从前往后处理每一棵树的形态,并回答询问,修改生长节点操作在 $l$ 处生效,在 $r+1$ 处失效.
简单画了一下,实心点是实点,空心点是虚点,虚点下面栽的子树就是后面生长出来的实点.
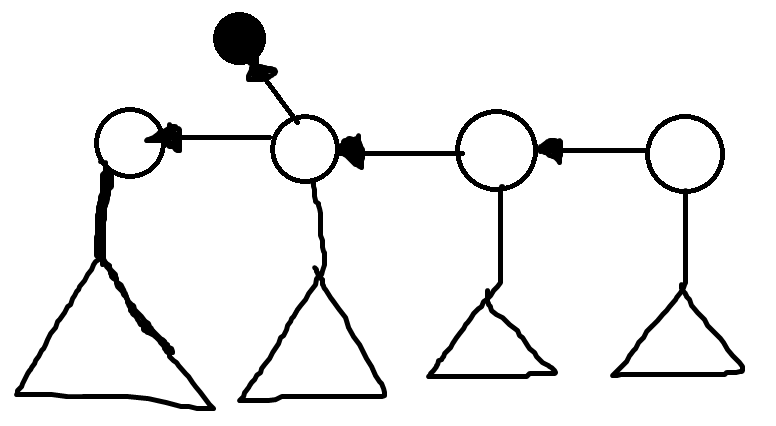
生效时,就把它的虚点栽到 $x$ 这个实点下面,这样后面长出来的点都在 $x$ 的子树中了.
失效时,就把它的虚点给移回去,即移回所有虚点按时间串好的那条链上.
回答询问时,将虚点权值设为 $0$ ,实点权值设为 $1$ ,答案就是两点路径上点权和 $-1$ .
因为我们维护的是有根树,不能用 makeroot 去改变它的形态,只能维护出每个点到根的路径点权之和 $sum(x)$ .
还需要找出 $x,y$ 的 LCA ,答案就是 $sum(x)+sum(y)-2sum(LCA)$ .
可以先 Access(x) ,再 Splay(x) ,再 Access(y) ,最后一次切换的虚边指向的点就是 LCA.
Loj 2434 历史
构造 + LCT 维护子树信息.
做过树点涂色那道题的话,马上就能看出 “崛起” 这个过程等同于 LCT 中的一次 Access 操作.
每个点的贡献可以分开算,若相邻两次 Access 操作来自它的两个不同的子树,或分别来自子树和自己,就有 $1$ 的贡献.
记 $A(u)$ 表示子树 $u$ 中共有多少次 Access 操作.
当 $u$ 的所有儿子 $v$ 的 $\max A(v)$ ,以及 $a(u)$ 都没有超过 $A(u)$ 的一半时,总可以交替安排,产生 $A(u)-1$ 的贡献.
否则,若它们中的最大值为 $mx$ ,最多就只能产生 $2(A(u)-mx)$ 的贡献.
直接这样做一遍树形 dp ,就可以完成预处理,考虑如何处理修改操作.
构造一下,若 $A(x)$ 超过了 $A(fa(x))$ 的一半,就设 $fa(x)\to x$ 为实边,否则为虚边.
每个点最多只会有 $1$ 个实儿子,形成了一个实虚链的剖分,用 LCT 来维护这个东西,以及权值的子树和,即 $A(u)$ .
修改只会让 $a$ 增大,修改 $x$ 时, $x$ 到根的路径上实边不会变成虚边,它们的贡献也不变,因为 $A(u),mx$ 增加的值相同.
那么只有虚边可能变成实边,每次用 Splay 操作跳过一条实链,判断虚边是否会变成实边,去修改它的贡献.
类似于树链剖分,可以证明 $x$ 到根路径上虚边数目是 $O(\log n)$ 的,那么每次修改操作的时间复杂度也是 $O(\log n)$ .