bzoj 1094 粒子运动

Posted on | Edited on | Views:

计算几何的一些基础操作.

为了后续处理起来方便,可以先将坐标系平移,使得圆心成为坐标系的原点.

考虑枚举两个点,计算它们在移动过程中出现的最近距离来更新答案.

每个点的运动路径是 $k$ 条线段组成的折线,考虑先把这 $k$ 条线段的起止位置,时间都算出来.

尝试去模拟点的运动,通过解方程可以确定在哪里撞上边界,撞上后需要更新速度.

假设交点是 $B$ ,先找到 $A$ 满足 $\vec{AB}=\vec v$ ,求出交点处的法线,把 $A$ 沿着它对称过去得到 $A’$ ,则新的速度为 $\vec{BA’}$ .

点关于直线 $y=\tan\theta \cdot x$ 的对称可以通过角度的运算实现,用 $\alpha,\beta$ 分别表示对称前后的极角,则 $\beta=2\theta-\alpha​$ .

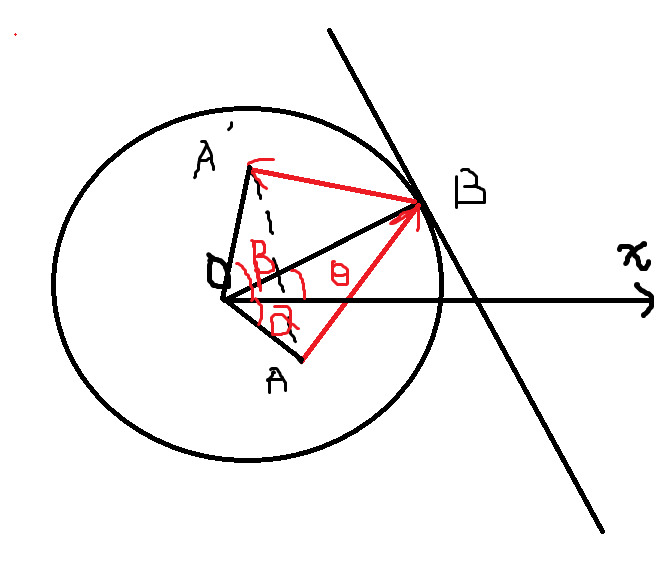
这样可以求出一个点的 $k$ 条线段的信息.

考虑两个点的最近距离,每个点有 $k$ 个关键时间点,所以最多需要考虑 $2k$ 个时间段.

每个时间段内两个点的方向都不会变,设 $t$ 表示「当前时刻 - 该时间段开始的时刻」,则距离的平方是 $t$ 的二次函数.

用二次函数在区间内求最小值的方法,就可以求出该时间段内两点的最近距离,注意可能有退化成一次函数的情况.

时间复杂度 $O(n^2\cdot k)$ .

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
//%std
#include<bits/stdc++.h>
#define endl '\n'
using namespace std;
typedef long long ll;
inline int read()
{
	int out=0,fh=1;
	char jp=getchar();
	while ((jp>'9'||jp<'0')&&jp!='-')
		jp=getchar();
	if (jp=='-')
		fh=-1,jp=getchar();
	while (jp>='0'&&jp<='9')
		out=out*10+jp-'0',jp=getchar();
	return out*fh;
}
const double inf=2e9,Pi=acos(-1.0),eps=1e-8;
const int N=100+10;
int n,k;
struct v2
{
	double x,y;
	v2(double x=0,double y=0):x(x),y(y) {}
	v2 operator + (const v2 &rhs) const
	{
		return v2(x+rhs.x,y+rhs.y);
	}
	v2 operator - (const v2 &rhs) const
	{
		return v2(x-rhs.x,y-rhs.y);
	}
	v2 operator * (const double &k) const
	{
		return v2(k*x,k*y);
	}
	double modulus()
	{
		return sqrt(x*x+y*y);
	}
}p[N],v[N];
double sqr(double x)
{
	return x*x;
}
double R,cx,cy,ans=inf;
void report(double x)
{
	ans=min(ans,x);
}
v2 st[N][N],vec[N][N];
double t[N][N];
double solve(double x,double y,double vx,double vy)
// (x+t*vx)^2+(y+t*vy)^2=R^2
{
	double a,b,c;
	a=vx*vx+vy*vy;
	b=2*x*vx+2*y*vy;
	c=x*x+y*y-R*R;
	double delta=b*b-4*a*c;
	// assert(delta>0);
	return (-b+sqrt(delta))/(2*a);
}
v2 reflect(v2 vel,v2 pos)
{
	v2 A=pos-vel;
	double dist=A.modulus();
	double alpha=atan2(A.y,A.x);
	double theta=atan2(pos.y,pos.x);
	double beta=2*theta-alpha;
	if(beta>2*Pi)
		beta-=2*Pi;
	return v2(dist*cos(beta),dist*sin(beta))-pos;
}
void init(int i)
{
	v2 pos=p[i],vel=v[i];
	double tim=0;
	for(int j=1;j<=k+1;++j)
	{
		st[i][j]=pos,t[i][j]=tim,vec[i][j]=vel;
		if(j>k)
			break;
		double tc=solve(pos.x,pos.y,vel.x,vel.y);
		tim+=tc;
		pos=pos+vel*tc;
		vel=reflect(vel,pos);
	}
}
double MinDist(double T,v2 pa,v2 pb,v2 va,v2 vb)
// t \in [0,T] , Dist^2=at^2+bt+c
{
	double a=sqr(va.x-vb.x)+sqr(va.y-vb.y);
	double b=2*(va.x-vb.x)*(pa.x-pb.x)+2*(va.y-vb.y)*(pa.y-pb.y);
	double c=sqr(pa.x-pb.x)+sqr(pa.y-pb.y);
	double x;
	if(fabs(a)<eps)
	{
		if(b>0)
			x=0;
		else
			x=T;
	}
	double mid=-b/(2*a);
	if(0<=mid && mid<=T)
		x=mid;
	else
	{
		if(mid<0)
			x=0;
		else
			x=T;
	}
	return sqrt(a*x*x+b*x+c);
}
void calc(int i,int j)
{
	int k1=1,k2=1;
	while(k1<=k && k2<=k)
	{
		double Tmin=max(t[i][k1],t[j][k2]);
		double Tmax=min(t[i][k1+1],t[j][k2+1]);
		v2 pa=st[i][k1]+vec[i][k1]*(Tmin-t[i][k1]);
		v2 pb=st[j][k2]+vec[j][k2]*(Tmin-t[j][k2]);
		report(MinDist(Tmax-Tmin,pa,pb,vec[i][k1],vec[j][k2]));
		if(t[i][k1+1]<t[j][k2+1])
			++k1;
		else
			++k2;
	}
}
int main()
{
	scanf("%lf%lf%lf",&cx,&cy,&R);
	n=read(),k=read();
	for(int i=1;i<=n;++i)
	{
		scanf("%lf%lf%lf%lf",&p[i].x,&p[i].y,&v[i].x,&v[i].y);
		p[i].x-=cx;
		p[i].y-=cy;
	}
	for(int i=1;i<=n;++i)
		init(i);
	for(int i=1;i<n;++i)
		for(int j=i+1;j<=n;++j)
			calc(i,j);
	printf("%.3f\n",ans);
	return 0;
}