CF1181

Posted on | Views:

$Div.2$

鸽了生物晚自习过来打.

A Chunga-Changa

  • 签到题.分类讨论一下就好了.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
inline ll read()
{
	ll out=0,fh=1;
	char jp=getchar();
	while ((jp>'9'||jp<'0')&&jp!='-')
		jp=getchar();
	if (jp=='-')
		fh=-1,jp=getchar();
	while (jp>='0'&&jp<='9')
		out=out*10+jp-'0',jp=getchar();
	return out*fh;
}
ll x,y,z;
int main()
{
	x=read(),y=read(),z=read();
	if((x+y)/z==x/z+y/z)
		cout<<(x+y)/z<<' '<<0<<endl;
	else
	{
		ll s=x/z+y/z;
		x%=z,y%=z;
		if((x+y)/z)
			cout<<s+1<<' '<<min(z-x,z-y)<<endl;
		else
			cout<<s<<0<<endl;
	}
	return 0;
}

B Split a Number

  • 显然应该贪心从最中间的位置切开.
  • 有 $0$ 的话,就从中间往两边分别找第一个合法的位置就好了.

高精度用 $python$ 就很棒.

1
2
3
4
5
6
7
8
9
10
11
12
13
n = input()
s = raw_input()
fig = []
for i in xrange(1, n):
    if s[i] != '0':
        fig.append((max(i, n - i), i))
fig.sort()
k = fig[0][0]
ans = int(s)
for i in xrange(min(10, len(fig))):
    j = fig[i][1]
    ans = min(ans, int(s[:j]) + int(s[j:]))
print ans

C Flag

  • 记录 $D(i,j)$ 表示从 $(i,j)$ 往下走,并且满足颜色一直相同能走到的最远位置, $k(i,j)$ 表示从 $(i,j)$ 往右走,并且满足颜色一直相同能走的最远格数.
  • 然后大力枚举 $(i,j)$ ,统计以 $(i,j)$ 为左上角的 $Flag$ 数目即可.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
inline int read()
{
	int out=0,fh=1;
	char jp=getchar();
	while ((jp>'9'||jp<'0')&&jp!='-')
		jp=getchar();
	if (jp=='-')
		fh=-1,jp=getchar();
	while (jp>='0'&&jp<='9')
		out=out*10+jp-'0',jp=getchar();
	return out*fh;
}
const int MAXN=1e3+10;
int n,m;
int col[MAXN][MAXN];
char buf[MAXN];
int D[MAXN][MAXN];
int k[MAXN][MAXN];
const int inf=1e9;
struct seg
{
	int val[MAXN<<2];
#define root val[o]
#define lson val[o<<1]
#define rson val[o<<1|1]
	void bd(int y,int o,int l,int r)
	{
		if(l==r)
		{
			root=k[l][y];
			return;
		}
		int mid=(l+r)>>1;
		bd(y,o<<1,l,mid);
		bd(y,o<<1|1,mid+1,r);
		root=min(lson,rson);
	}
	int query(int o,int l,int r,int L,int R)
	{
		assert(root);
		if(L<=l && r<=R)
			return root;
		int mid=(l+r)>>1;
		int s=inf;
		if(L<=mid)
			s=min(s,query(o<<1,l,mid,L,R));
		if(R>mid)
			s=min(s,query(o<<1|1,mid+1,r,L,R));
		assert(s>=1 && s<=m);
		return s;
	}
}T[MAXN];
ll calc(int x,int y)
{
	int p1=x;
	int p2=D[p1][y]+1;
	if(p2>n)
		return 0;
	int p3=D[p2][y]+1;
	if(p3>n)
		return 0;
	int len=p2-p1;
	if(p3!=p2+len)
		return 0;
	if(p3+len-1>n)
		return 0;
	if(D[p3][y]<p3+len-1)
		return 0;
	return T[y].query(1,1,n,p1,p3+len-1);
}
int main()
{
	n=read(),m=read();
	for(int i=1;i<=n;++i)
	{
		scanf("%s",buf+1);
		for(int j=1;j<=m;++j)
			col[i][j]=buf[j]-'a'+1;
	}
	for(int i=1;i<=n;++i)
	{
		for(int j=m;j>=1;--j)
			if(col[i][j]!=col[i][j+1])
				k[i][j]=1;
			else
				k[i][j]=k[i][j+1]+1;
	}
	for(int j=1;j<=m;++j)
	{
		for(int i=n;i>=1;--i)
			if(col[i][j]!=col[i+1][j])
				D[i][j]=i;
			else
				D[i][j]=D[i+1][j];
	}
	for(int j=1;j<=m;++j)
		T[j].bd(j,1,1,n);
	ll ans=0;
	for(int i=1;i<=n;++i)
		for(int j=1;j<=m;++j)
			ans+=calc(i,j);
	cout<<ans<<endl;
	return 0;
}

D Irrigation

  • 容易发现当所有的城市次数都相等后举办地点一定会出现循环 $1,2,3,\dots,m$ .
  • 记初始 $n$ 轮举办后,举办次数最多的一个城市举办了 $t$ 场,那么根据规则,再举办 $t\cdot m-n$ 场后,即从第 $t\cdot m+1$ 场开始举办城市就会开始出现循环 $1,2,3,\dots,m$ .
  • 可以将询问离线下来,按照时间从前往后顺序进行回答.
  • 一层一层填满下面这个图,边填边回答询问 ( $two\ pointer$ ),用 $treap$ 维护当前可能会被填到的元素就好了.

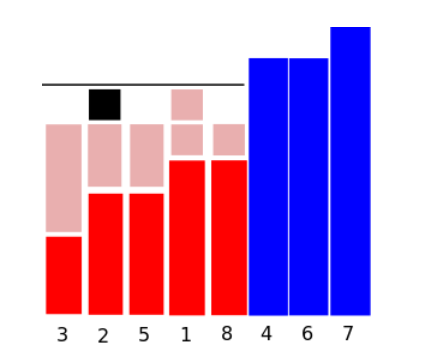
  • 最后还剩下的询问的答案一定是出现在 $1,2,3,\dots,m$ 的循环中,答案容易得出.

E A Story of One Country

  • 尝试倒着做,每次水平或竖直地将一个子矩形切成两个,并且切的时候不能切断任意一个 $castle$ 区域.
  • 如果经过若干次切割后,能使得每个子矩形内都包含了 恰好一个 $castle$ 区域,那么原图就是合法的.
  • 注意到对于同一个子矩形,如果把它内部的 $castle$ 区域用这个 $castle$ 区域的一个非空子集代替,不会使结果变劣,即,若原子矩形是合法的,那么替换后的子矩形仍然是合法的.
  • 又因为题目对切割次数没有限制,所以我们只要能找到一条切割线(水平或竖直)使得切割后得到的两个子矩形内部都含有 $castle$ 区域,且自身不穿过 $castle$ 区域,就称它是合法的,沿着它切开,不会影响最终的答案.
  • 于是我们可以递归解决这个问题,对于当前的子矩形每次找到一条切割线,切割后递归处理得到的两个子矩形.若当前矩形不是恰好包含一个 $castle$ 区域,又找不到合法的切割线,则说明当前子矩形不合法,原图也不合法.
  • 如果每次随意去找一条合法切割线执行上述操作,最坏情况是每次切割后,一个子矩形内只有 $1$ 个 $castle$ 区域,而另一个子矩形内含有剩下所有的 $castle$ 区域,此时的时间复杂度是 $O(n^2logn)$ ,只能通过简单版的数据.
  • 用线段树来维护 $castle$ 区域,每次找出合适的切割使得得到的两个子矩形含有的 $castle$ 区域数目差尽可能小,此时时间复杂度为 $O(nlog^2n)$ ,可以通过所有数据.